Circle of Fifths

Home About Code Projects eBook Merch Playlists Contact

Circle of Fifths Poster

The circle of fifths has become a foundational tool in Western music theory. Graphically, different alterations to the circle were made by Nikolay Diletsky in the 1670s, and Johann David Heinichen in 1728, until we finally arrived at the Circle of Fifths with which we are familiar today. The circle presents a way of traversing though all 12 keys by moving through successive perfect fifths or 7 semitones (eg. C to G) in a clockwise direction and perfect fourths or 5 semitones (eg. C to F) in an anti-clockwise direction. The movement of keys in fourths and fifths are the second and third most consonant intervals besides the octaves, thus making them the most harmonious movement in Western music.
Essentially the diagram is a rich map of the 12 key signatures we have in Western music and how they relate to each other. Each key can be seen as the tonal center of the major or minor modes. It explains how adjacent keys are the most similar to each other.

My diagram makes it easier for those who don't yet know how to read the staff but want to get started learning which chords you can play together, and what notes you can find in those chords. The usual circle of fiths usually assumes that you can read the treble cleff and that you know the notes in the major and minor triads already. Thus it is difficult for a non-musician or beginner to decipher the traditional circle of fifths, and even if a musician may know their triads, the traditional circle does not show Roman numerals, indicating where the seven harmonic degrees are that is the basis of the Nashville Number System. I believe this poster will be especially helpful for students of music who have not familiarised themselves with the piano, and have perhaps begun to learn guitar or bass or other stringed instruments where black and white keys are not immediately apparent.

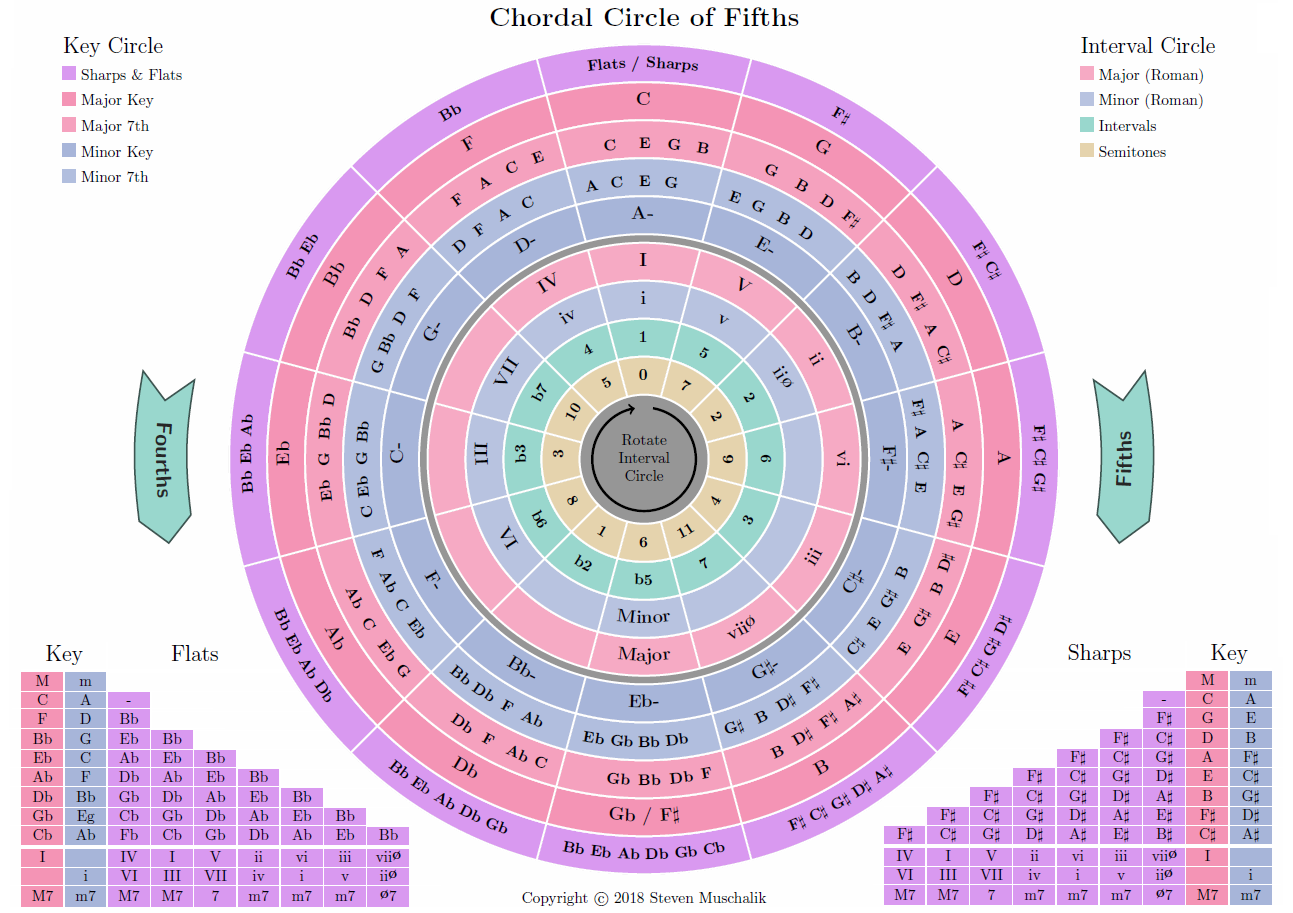
Free low-res Chordal Circle of Fifths Poster

Buy Now as PDF file for $3.99 AUD

As a quick theory refresher, Roman capital letters eg. I, IV, V on the interval circle refer to the corresponding major keys and the lowercase Roman letters eg. i, iv, v represent the corresponding minor keys.

To remind you how to harmonize the C major scale, the chords you can play are C, Dm, Em, F, G, Am, Bdim. So the major chords are C, F, G, the minor chords are Dm, Em, Am, and the diminished chord is Bdim.

Let's have a look at the most common I-IV-V chord progression on my Circle of Fifths and how you can use what I've called the Interval Circle. If you like you can print out the poster twice and cut out the Interval Circle so you can pin it onto the uncut poster. This will allow you to rotate the inner circle so that your I falls on the key or tonal centre of your scale.

For now, I will simply assume we are in the key of C major. If you locate the IV, I, V on the inner major interval circle, you will see they are all together side by side. The keys related to each of them are all the Perfect intervals. In other words, the notes F, C, and G are perfect relative to C. They also all produce major chords F, C, and G major. Now clockwise from ii, vi, iii you will find notes which produce the minor chords Dm, Am, and Em. Finally, almost opposite to I you will find the last type of chord you can harmonize with I, the viiø, which is the diminished chord, in this case, Bdim. Alternatively, you can also look at the relative minor keys below the chords indicated by the IV, I, V. You would find they relate to the minor chords Dm, Am, Em. Looking below the ii chord relating to the Dm in the major inner circle you'd see the parallel iio under the minor inner circle, which means you could play Bdim. As you can see, just using the I-IV-V (C-F-G)chords from the major inner circle, and the i-iv-v (Am-Dm-Em) from the minor inner circle gives you six different chords you could play.

Theoretically, all the remaining notes located mostly anti-clockwise to I, that are not on the 7-notes of the inner major interval circle start on the notes of minor intervals, for example, b7, b3, b6, b2, b5. See the green inner interval circle. As you move further from I, starting on major chords Bb, Eb, Ab, Db, Gb, you would be moving further and further away harmonically from the key. When you reach b5 (Gb), which is opposite to I, you will be a tritone and 6 semitones away. The tritone interval is so dissonant that it was named 'The Devil's Interval' and was avoided for centuries by composers. However, with time it was used in classical music to prepare you for something sinister or evil or to provide a spooky atmosphere. Rock and metal music often employed the tritone to generate tension which made the music sound unsettling or alternatively exciting.

The Circle of Fifths describes how each stepwise movement further away from C in the circle adds one new sharp in a clockwise direction, and one new flat is added for each move in the anti-clockwise direction. Moving clockwise through the 12 keys starting on F you get the keys:

F C G D A E B F# C# G# D# A# or
F C G D A E B Gb Db Ab Eb Bb

The Circle of Fifths maps onto a 12-hour clock, as described in the following table below. No key signature has both sharps and flats. Now, as you move through each key beyond C at 0 am, new sharps or flats will be added to the key. For instance, the difference between C major at 0 pm and G major at 1 pm, is that F toggles to F sharp. To get to the next key, D major at 2 pm, you toggle the C to C sharp. In the key of A at 3 pm, you toggle the G to G sharp. To become fluent with Western music, you should learn these patterns by heart, in the same way, you must learn your times' tables to do the most basic maths.

As you turn clockwise the order of flats is
F#, C#, G#, D#, A#, E#

As you turn anti-lockwise the order of flats is:
Bb, Eb, Ab, Db, Gd, Cb

Here is a little tip to remember the pattern. You will notice that the pattern of sharps F-C-G-D-A-E-B appears when going clockwise from C, and the pattern of flats B-E-A-D-G-C-F appears when going counterclockwise from C. The pattern is mirror reversed when you change from a clockwise movement to an anti-clockwise movement.

Major and minor keys that have the same number of either sharps or flats are considered relatives. For example, C major's relative minor is in A because C major has the exact same notes as A minor.

Clock Position	No #/b	New Sharp/Flat	Sharps / Flats	Major Scale	Relative Minor
0am	0 sharps	-	-	C Major	A Minor
1pm	1 sharps	F# added	F#	G Major	E Minor
2pm	2 sharps	C# added	F# C#	D Major	B Minor
3pm	3 sharps	G# added	F# C# G#	A Major	F# Minor
4pm	4 sharps	D# added	F# C# G# D#	E Major	C# Minor
5pm	5 sharps	A# added	F# C# G# D# A#	B Major	G# Minor
6pm	6 sharps	Cb added	A# D# G# C# F# B Bb Eb Ab Db Gb Cb	Gb / F# Major	Eb Minor
7pm	5 flats	Gb added	Bb Eb Ab Db Gb	Db Major	Bb Minor
8pm	4 flats	Db added	Bb Eb Ab Db	Ab Major	F Minor
9pm	3 flats	Ab added	Bb Eb Ab	Eb Major	C Minor
10pm	2 flats	Eb added	Bb Eb	Bb Major	G Minor
11pm	1 flats	Bb added	Bb	F Major	D Minor

What are some quick ways to find important notes on the clock if you've learned the circle of fifths by heart, especially if you picture the circle as a clock in your mind or if you have memorised the sequence of letters?
How do you find the relative minor of a major key? You count 3 steps clockwise from I. So if you are in the key of C at 0am, just add 3hrs and you'll land on A at 3pm.
How do you find the perfect fifth of I? Just add 1hr on the clock. So if you are in the key of C at 0am, then go to 1pm, where the G is located.
How do you find the perfect fourth of I? If you are in C at 0am, then subtract 1hr, and move anti-clockwise by one step to 11am where F is located.
How do you find the third of I? If you are in C at 0am, then add 4hrs eg to get to 4pm, which is where E is located.

The Circle of Fifths can also be used as an analytical tool to describe the darkness and brightness of the seven chords or modes of the major scale relative to the root. As Anton Schwartz describes, the major modes gradually become darker though Lydian, Ionian, Mixolydian, Dorian, Aeolian, Phrygian and Locrian. Each of these modes of the major scale traces out seven consecutive places on the Circle of Fifths. In this way, with each move in the circle, the brightest note is replaced with the next darkest note relative to the root note. Thus, relative to C, the notes F#, C, Bb, Eb, Ab, Db, Gb become increasingly darker sounding.

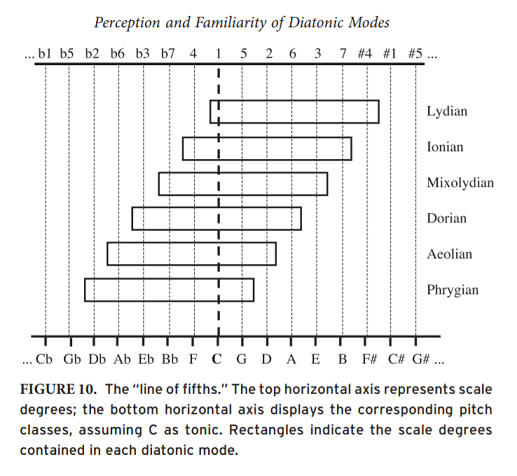
In the paper Perception and Familiarity of Diatonic Modes by Dephane Tan & David Temperley, I discovered this nice graphic showing the circle of fifths in a linear form with the intervals and notes mapped out as in fifths. The graphic represents the modes of the major scale on this linear line of fifths. You can of course also imagine this on the Circle of Fifths.

Ethan Hein says that one can imagine the seven-tone major scale and its modes as a series of toggles. Each note beside the root can be flat/sharp or natural. If you toggle a natural note (except the 4th), you produce a scale with a darker feeling, and if you toggle a flat note, you give the scale a brighter feeling. For example, relative to the major scales with the toggles on 1, 2, 3, 4, 5, 7, the minor scale sounds darker, with its intervals toggled to 1, 2, b3, 4, 5, b6, b7. The Lydian scale with the intervals 1, 2, 3, #4, 5, 7 sounds even brighter than the major scale.

Scale Interval Toggles							Brightness
1	2	3	#4	5	6	7	Brightest Intervals
1	b2	b3	4	b5	b6	b7	Darkest Intervals
2	6	4	1	7	5	3	Rank

Lydian							Brightness
1	2	3	#4	5	6	7	Lydian
1	b2	b3	4	b5	b6	b7

Major							Brightness
1	2	3	#4	5	6	7	Major
1	b2	b3	4	b5	b6	b7

Minor							Brightness
1	2	3	#4	5	6	7	Minor
1	b2	b3	4	b5	b6	b7

Modes of the Major Scale and their Brightness
No of #/b	Mode	Modes	Intervals	Notes	Sharps / Flats	Major Scale	Brightness
1	IV	C Lydian	1 2 3 #4 5 6 7	C D E F# G A B	F#	G Major	Brighest
0	I	C Ionian	1 2 3 4 5 6 7	C D E F G A B	-	C Major
1	V	C Mixolydian	1 2 3 4 5 6 b7	C D E F G A Bb	Bb	F Major
2	ii	C Dorian	1 2 b3 4 5 6 b7	C D Eb F G A Bb	Bb Eb	Bb Major	Middle
3	vi	C Aeolian	1 2 b3 4 5 b6 b7	C D Eb F G Ab Bb	Bb Eb Ab	Eb Major
4	iii	C Phrygian	1 b2 b3 4 5 b6 b7	C Db Eb F G Ab Bb	Bb Eb Ab Db	Ab Major
5	vii	C Locrian	1 b2 b3 4 b5 b6 b7	C Db Eb F Gb Ab Bb	Bb Eb Ab Db Gb	Db Major	Darkest

Consequently, we could also say that the order of brightness to darkess for chords in a major scale are: IV, I, V, ii, vi, iii, vii.

We can see that if you look at the type of chord produced, we have three major chords (IV, I, V) sounding the brightest, followed by three minor chords (ii, vi, iii), followed by a diminished chord (vii). According to the empirical rank order of consonance we have:

Major > Minor > Diminished > Augmented

Looking at the difference between the brightest mode (Lydian) and the darkest mode (Locrian), the Lydian mode consist of a maximum of major and augmented steps (M2, M3, A4, P5, M6, M7) and the Locrian mode consist of a maximum of minor and diminished steps (m2, m3, P4, dim5, m6, m7). Thus the darkness-consonance logic of the Circle of Fifths coincides well with our perception that major chords are more consonant than minor chords and that diminished chords are more dissonant than minor chords. For more details see The Psychophysics of Harmony Perception: Harmony is a Three-Tone Phenomenon.

As you can see, there is a lot of wisdom packed into the Circle of Fifths which was fashioned on the major scale and its modes. Unfortunately, trying to map the logic of the Circle of Fifths on to other scales outside of the major modes is not as straightforward. For example, the Harmonic Minor and the Dorian mode both have an equal number of flats, but do not sound equally dark.
1 2 b3 4 5 b6 7 Harmonic Minor
1 2 b3 4 5 6 b7 Dorian

It is perhaps these kinds of investigations into the possible colours found in harmony which lead jazz composer George Russell to explore the 'Lydian Chromatic Concept of Tonal Organization' based on the tonal gravity of the Lydian mode.

Finally, for the mathematically minded, the history of the early versions of the circle of fifths is interesting. In the sixth century, B.C. Pythagoras developed the Pythagorean Circle to deduce how to space the intervals using successive perfect fifths with a ratio of 3/2 which was deemed as the most consonant interval after the octave with a ratio of 2/1. According to the Greeks, a series of 12 perfect fifths should arrive back at the same pitch, albeit 7 perfect octaves away, however, it is mathematically not possible to do this using simple ratios.
In Pythagorean tuning the ratio used to tune fifths is r_p = 3/2 = 1.5, whereas today's modern equal temperament uses the 12th root of 2^7 as its ratio r_e to calculate the fifth (7th semitone) = 2^(7/12) = 1.498
r_p= 3/2 = 1.5
r_e = 12th sqrt(128) = 1.498307

Using the circle of fifths r_p ratio multiplying 3/2 with itself twelve times = (3/2)^12 = 531441/4096 = 128 + 3057/4096 whereas the mathematically correct r_e ratio 2^(7/12) to the power of 12 = (2^(7/12))^12 = 2^7 = 128. We call the difference between these two tuning systems the Pythagorean comma.